/Szkoła średnia/Zadania testowe/Ciągi/Arytmetyczny

Zadanie nr 9518725

Dodaj do ulubionych
Dodaj do rozwiązanych

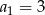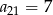W ciągu arytmetycznym a1 = 3 oraz a21 = 7 . Wtedy suma 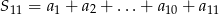S 11 = a1 + a 2 + ...+ a10 + a 11 jest równa
A) 44 B) 88 C) 46 D) 55

Rozwiązanie

Sposób I

Z podanych informacji mamy

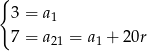
{ 3 = a1 7 = a21 = a1 + 20r

Dodając te równości stronami mamy

10 = 2a + 2 0r ⇒ 5 = a + 10r = a . 1 1 11

Korzystamy teraz ze wzoru

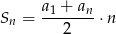
a1 +-an- Sn = 2 ⋅ n

na sumę n początkowych wyrazów ciągu arytmetycznego. Mamy zatem

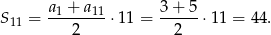
a1 +-a11 3-+-5- S 11 = 2 ⋅ 11 = 2 ⋅11 = 44.

Sposób II

Ze wzoru 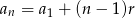an = a1 + (n − 1)r na n -ty wyraz ciągu arytmetycznego mamy

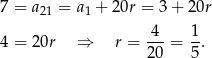
7 = a21 = a1 + 20r = 3 + 20r 4 1 4 = 20r ⇒ r = ---= -. 20 5

Korzystamy teraz ze wzoru na sumę n początkowych wyrazów ciągu arytmetycznego.

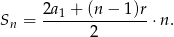
2a + (n − 1)r Sn = --1------------⋅n. 2

Mamy zatem

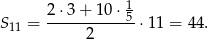
2 ⋅3 + 10 ⋅ 1 S11 = -----------5 ⋅11 = 4 4. 2

 
Odpowiedź: A

Wersja PDF