/Szkoła średnia/Zadania testowe/Ciągi/Arytmetyczny

Zadanie nr 9620576

Dodaj do ulubionych
Dodaj do rozwiązanych

Suma dwudziestu początkowych wyrazów pewnego ciągu arytmetycznego jest 6 razy większa od sumy dziesięciu początkowych wyrazów tego ciągu. Wynika stąd, że suma drugiego i czwartego wyrazu tego ciągu jest równa
A) 0 B) 2 C) 8 D) 6

Rozwiązanie

Ze wzoru 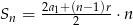2a1+(n−1)r Sn = 2 ⋅ n na sumę początkowych wyrazów ciągu arytmetycznego otrzymujemy równanie

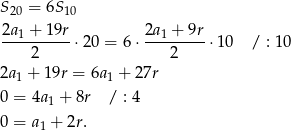
S20 = 6S 10 2a-1 +-19r 2a1 +-9r- 2 ⋅20 = 6⋅ 2 ⋅10 / : 10 2a1 + 19r = 6a 1 + 2 7r 0 = 4a 1 + 8r / : 4 0 = a1 + 2r.

Mamy więc

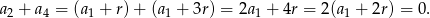
a 2 + a4 = (a1 + r) + (a1 + 3r) = 2a1 + 4r = 2 (a1 + 2r ) = 0.

 
Odpowiedź: A

Wersja PDF