/Szkoła średnia/Zadania testowe/Funkcje - wykresy/Dany wykres

Zadanie nr 2522004

Dodaj do ulubionych
Dodaj do rozwiązanych

Na rysunku przedstawiono fragment wykresu funkcji 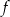f określonej dla każdej liczby rzeczywistej x .

PIC

Jeden spośród podanych poniżej wzorów jest wzorem tej funkcji. Wskaż wzór funkcji 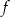f .
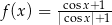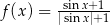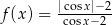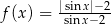
A) f(x ) = -cosx+-1- |cosx|+ 1 B) f(x) = sinx+1-- |sinx|+1 C) f(x ) = |ccoossxx|−−22- D) |sin-x|−2- f (x) = sinx− 2

Rozwiązanie

Sposób I

Widać, że dany wykres jest wykresem funkcji parzystej – to eliminuje dwie odpowiedzi z sinusami. Ponadto widać, że funkcja 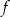f nie ma miejsc zerowych, co eliminuje odpowiedź

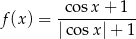
f(x) = -co-sx-+-1- | cosx| + 1

bo ta funkcja ewidentnie ma miejsca zerowe – na przykład 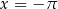x = − π . W takim razie na wykresie przedstawiono wykres funkcji

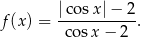
|co-sx|−--2 f (x) = cos x− 2 .

Sposób II

Z wykresu widać, że 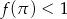f(π ) < 1 , co łatwo eliminuje odpowiedzi z sinusami (bo 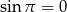sin π = 0 ). Ponadto

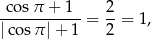
-cosπ-+--1-- 2- |cosπ |+ 1 = 2 = 1,

więc poprawną odpowiedzią musi być

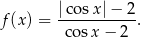
|co sx|− 2 f (x) = -----------. cos x− 2

 
Odpowiedź: C

Wersja PDF