Zadanie nr 4255543
Liczba  jest rozwiązaniem równania
jest rozwiązaniem równania 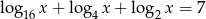 . Zatem
. Zatem
A) 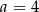 B)
B) 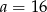 C)
C) 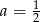 D)
D) 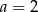
Rozwiązanie
Sposób I
Przekształćmy dane równanie – zmieniamy podstawy wszystkich logarytmów na 2.
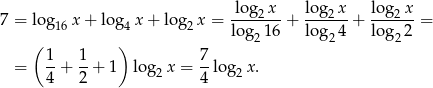
Mamy stąd 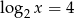 , czyli
, czyli 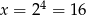 .
.
Sposób II
Przekształćmy dane równanie – zmieniamy podstawy wszystkich logarytmów na  korzystając ze wzoru
korzystając ze wzoru
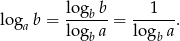
Liczymy
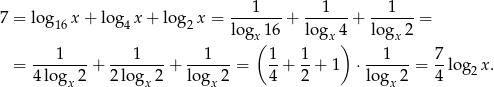
Mamy stąd 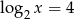 , czyli
, czyli 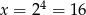 .
.
Odpowiedź: B

