Zadanie nr 1855693
Rozważamy wszystkie kody czterocyfrowe utworzone tylko z cyfr 1, 3, 6, 8, przy czym w każdym kodzie każda z tych cyfr występuje dokładnie jeden raz. Liczba wszystkich takich kodów jest równa
A) 4 B) 10 C) 24 D) 16
Rozwiązanie
Sposób I
Różnych ustawień (permutacji) 4 cyfr jest
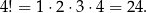
Sposób II
Pierwszą cyfrę tworzonego kodu możemy wybrać na 4 sposoby, drugą cyfrę na 3 sposoby, trzecią na 2 sposoby, a przy ostatniej cyfrze nie mamy już wyboru. Są więc
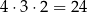
takie kody.
Odpowiedź: C

