/Szkoła średnia/Zadania testowe/Kombinatoryka

Zadanie nr 3402001

Dodaj do ulubionych
Dodaj do rozwiązanych

Ile jest wszystkich liczb naturalnych dodatnich mniejszych od 2021, których cyfra jedności jest jedną z cyfr: 0, 2, 6, 8?
A) 1010 B) 808 C) 606 D) 560

Rozwiązanie

Wszystkie liczby parzyste mniejsze od 2021 to

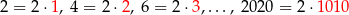
2 = 2 ⋅1, 4 = 2⋅ 2, 6 = 2⋅3 ,... , 2020 = 2⋅ 1010

Jest ich więc 1010. Wśród nich liczby kończące się cyfrą 4 to

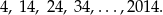
4, 14 , 24, 34,...,201 4.

Wypisane wyżej liczby to wyrazy ciągu arytmetycznego o różnicy 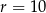r = 10 i pierwszym wyrazie 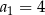a1 = 4 . Sprawdźmy którym wyrazem jest 2014.

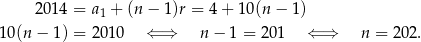
2014 = a1 + (n − 1)r = 4+ 10(n − 1) 10(n − 1) = 2010 ⇐ ⇒ n − 1 = 201 ⇐ ⇒ n = 202.

Są w takim razie 202 liczby naturalne mniejsze od 2021, które mają cyfrę jedności 4 i wszystkich liczb spełniających warunki zadania jest

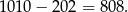
1010 − 20 2 = 808.

 
Odpowiedź: B

Wersja PDF