Zadanie nr 3541224
Ile jest wszystkich liczb naturalnych mniejszych od 500 utworzonych z cyfr: 1, 3, 5, 7, 9 (cyfry mogą się powtarzać)?
A) 125 B) 80 C) 75 D) 50
Rozwiązanie
Liczb jednocyfrowych jest 5. Liczb dwucyfrowych jest
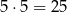
(każdą z cyfr możemy wybrać na dwa sposoby). Zastanówmy się nad liczbami trzycyfrowymi. Pierwszą cyfrę takiej liczby możemy wybrać na 2 sposoby (musi być to 1 lub 3), a każdą z pozostałych dwóch cyfr na 5 sposobów. Jest więc
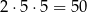
liczb trzycyfrowych spełniających warunki zadania. W sumie jest więc
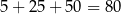
takich liczb.
Odpowiedź: B

