/Szkoła średnia/Zadania testowe/Kombinatoryka

Zadanie nr 5225159

Dodaj do ulubionych
Dodaj do rozwiązanych

Ile jest wszystkich liczb naturalnych czterocyfrowych mniejszych od 2018 i podzielnych przez 5?
A) 402 B) 403 C) 203 D) 204

Rozwiązanie

Sposób I

Liczby czterocyfrowe mniejsze od 2018 podzielne przez 5 to

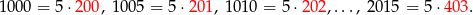
1000 = 5 ⋅200, 1005 = 5⋅2 01, 1 010 = 5 ⋅202,..., 2015 = 5⋅4 03.

Jest ich więc 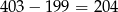403 − 199 = 204 .

Sposób II

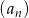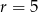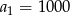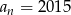Czterocyfrowe liczby podzielne przez 5 tworzą ciąg arytmetyczny (an) o różnicy r = 5 , w którym a1 = 1 000 i an = 2 015 . Mamy zatem

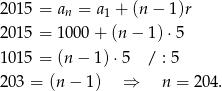
2015 = an = a1 + (n− 1)r 2015 = 1 000+ (n − 1) ⋅5 1015 = (n − 1)⋅5 / : 5 203 = (n − 1 ) ⇒ n = 204 .

 
Odpowiedź: D

Wersja PDF