Zadanie nr 5337476
Trzech panów i 
pań można ustawić w jednym rzędzie na 12 sposobów, tak aby osoby tej samej płci nie stały obok siebie. Liczba 
pań jest równa
A) 8 B) 4 C) 5 D) 2
Rozwiązanie
Jeżeli panie nie mogą stać obok siebie to muszą być porozdzielane panami. Panów jest tylko 3, więc mogą być co najwyżej 4 panie.
Jeżeli są 4 panie, to dwie z nich muszą stać na skrajnych miejscach, a dwie pomiędzy panami. Panie można ustawić na
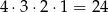
sposoby (pierwszą na 4 sposoby, drugą na 3 itd.), a panów na
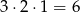
sposobów. W sumie są
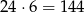
możliwości. Jest to wyraźnie za dużo, więc muszą być 2 panie (bo wyeeliminowaliśmy inne odpowiedzi).
Sprawdźmy jeszcze (choć nie musimy tego robić), że dla dwóch pań jest OK.
Jeżeli są 2 panie, to muszą stać między panami, których jak wcześniej zauważyliśmy można ustawić na 6 sposobów. Dwie panie można ustawić na 2 sposoby, więc w sumie jest
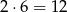
możliwości.
Odpowiedź: D
