Zadanie nr 5427382
Ile jest liczb naturalnych dwucyfrowych mniejszych od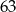 
, które mają dwie różne cyfry?
A) 45 B) 48 C) 63 D) 58
Rozwiązanie
Są trzy liczby z 6 na początku: 62, 61 i 60.
Policzmy teraz liczby z pierwszą cyfrą mniejszą od 6. Pierwszą cyfrę możemy wybrać na 5 sposobów, bo może być to jedna z liczb:
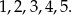
Druga cyfra nie może być równa pierwszej cyfrze, więc mamy 9 możliwości (może też być 0). W sumie jest więc
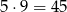
liczb z pierwszą cyfrą mniejszą od 6.
Razem jest
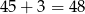
takich liczb.
Odpowiedź: B
