Zadanie nr 6063155
Liczby 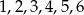 ustawiamy losowo w ciąg. Wszystkich możliwych ustawień takich, że liczby 1, 3 i 6 sąsiadują ze sobą (w dowolnej kolejności), jest
ustawiamy losowo w ciąg. Wszystkich możliwych ustawień takich, że liczby 1, 3 i 6 sąsiadują ze sobą (w dowolnej kolejności), jest
A) 72 B) 40 C) 192 D) 144
Rozwiązanie
Najpierw zastanówmy się na ile sposobów ustawić cyfry 1, 3 i 6 tak, aby spełniały założenia. Wyobraźmy sobie pola w które wpisujemy kolejne cyfry

Musimy policzyć na ile sposobów możemy wybrać pola dla cyfr 1, 3 i 6. Licząc od lewej możemy wybrać:
pierwsze, drugie, trzecie;
drugie, trzecie, czwarte,
trzecie, czwarte, piąte,
czwarte, piąte, szóste.
Są zatem 4 możliwości. Musimy jeszcze ustalić kolejność cyfr: 1,3,6, co możemy zrobić na 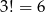 sposobów. Są więc w sumie
sposobów. Są więc w sumie
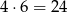
sposoby umieszczenia 1,3 i 6.
Układ pozostałych cyfr nie ma znaczenia, więc możemy ustawić je na pozostałych polach na
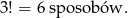
W sumie są więc
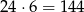
możliwe ustawienia.
Odpowiedź: D

