/Szkoła średnia/Zadania testowe/Kombinatoryka

Zadanie nr 7719451

Dodaj do ulubionych
Dodaj do rozwiązanych

Wszystkich liczb dwucyfrowych o różnych cyfrach jest
A) 90 B) 81 C) 82 D) 80

Rozwiązanie

Sposób I

Pierwszą cyfrę takiej liczby możemy wybrać na 9 sposobów – nie może być 0, a drugą też na 9 sposobów – może być 0, ale nie może być cyfra wybrana na pierwszym miejscu. Jest więc

9 ⋅9 = 81

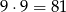
takich liczb.

Sposób II

Wszystkich liczb dwucyfrowych jest

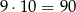
9⋅1 0 = 90

(pierwszą cyfrę możemy wybrać na 9 sposobów – nie może być 0, a drugą cyfrę można wybrać na 10 sposobów). Od tej liczby musimy odjąć liczby dwucyfrowe o tych samy cyfrach. Wypiszmy je

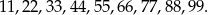
11,22,33,44 ,55,66,77,88 ,9 9.

Zatem wszystkich liczb dwucyfrowych o różnych cyfrach jest

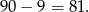
90 − 9 = 81 .

 
Odpowiedź: B

Wersja PDF