/Szkoła średnia/Zadania testowe/Kombinatoryka/Zbiory liczb

Zadanie nr 2953819

Dodaj do ulubionych
Dodaj do rozwiązanych

Ile jest wszystkich liczb naturalnych trzycyfrowych podzielnych przez 12 i niepodzielnych przez 8?
A) 20 B) 38 C) 75 D) 35

Rozwiązanie

Trzycyfrowe liczby podzielne przez 12 to

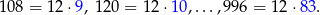
108 = 1 2⋅9, 120 = 12⋅ 10,...,996 = 12 ⋅83 .

Jest ich więc 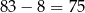83− 8 = 75 . Liczby podzielne przez 12 i 8 to liczby podzielne przez 24, czyli liczby:

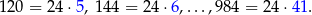
1 20 = 24 ⋅5, 144 = 24 ⋅6,...,984 = 24⋅ 41.

W sumie jest więc 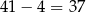41− 4 = 37 liczb trzycyfrowych podzielnych przez 24.

Liczb spełniających warunki zadania jest więc 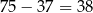75− 37 = 38 .  
Odpowiedź: B

Wersja PDF