/Szkoła średnia/Zadania testowe/Kombinatoryka/Zbiory liczb

Zadanie nr 6807149

Dodaj do ulubionych
Dodaj do rozwiązanych

Siedmiocyfrowe numery telefonów w pewnym mieście są tworzone z cyfr: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9, przy czym numery nie mogą zaczynać się od cyfr 0, 1, 9. Ile najwięcej takich numerów telefonicznych można utworzyć?
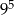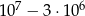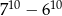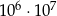
A) 5 9 B) 7 6 10 − 3 ⋅10 C) 10 10 7 − 6 D) 6 7 1 0 ⋅10

Rozwiązanie

Sposób I

Ponieważ pierwsza cyfra nie może być równa 0, 1 ani 9, więc możemy ją wybrać na 7 sposobów. Natomiast pozostałe 6 cyfr może być już dowolne. Ponieważ każdą z nich możemy wybrać na 10 sposobów, więc 6 cyfr możemy wybrać na

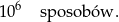
106 sposob ów .

Zatem liczba numerów jakie możemy utworzyć wynosi

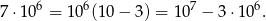
7⋅ 106 = 106(10 − 3) = 107 − 3⋅10 6.

Sposób II

Wszystkich możliwych numerów jest

107.

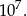
Numerów zaczynających się cyfrą 0 jest

106.

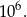
Tyle samo jest też numerów zaczynających się cyframi 1 i 9.

Zatem liczba numerów telefonów spełniających warunki zadania jest równa

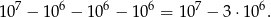
1 07 − 1 06 − 1 06 − 106 = 107 − 3 ⋅106.

 
Odpowiedź: B

Wersja PDF