/Szkoła średnia/Zadania testowe/Geometria/Stereometria

Zadanie nr 4176924

Dodaj do ulubionych
Dodaj do rozwiązanych

Suma długości wszystkich krawędzi sześcianu jest o 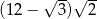√ --√ -- (12 − 3) 2 większa od długości przekątnej tego sześcianu. Pole powierzchni tego sześcianu jest równe
A) 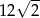√ -- 12 2 B) 12 C) 2 D)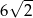 √ -- 6 2

Rozwiązanie

Jeżeli dorysujemy przekątną

PIC

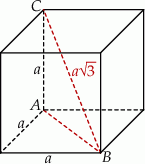
kwadratu w podstawie to powinno być jasne, że

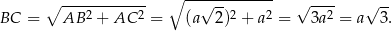
∘ ------------ ∘ ---√--------- √ ---- √ -- BC = AB 2 + AC 2 = (a 2)2 + a 2 = 3a2 = a 3.

Mamy więc

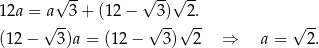
-- -- -- 12a = a √ 3+ (12− √ 3)√ 2. √ -- √ --√ -- √ -- (12 − 3)a = (1 2− 3) 2 ⇒ a = 2.

Pole powierzchni sześcianu jest 6 razy większe od pola pojedynczej ściany, więc jest równe

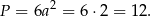
2 P = 6a = 6⋅2 = 12.

 
Odpowiedź: B

Wersja PDF