Zadanie nr 9947664
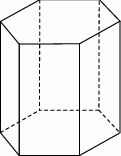
Liczba wszystkich krawędzi graniastosłupa jest o 12 większa od liczby wszystkich jego ścian bocznych. Stąd wynika, że podstawą tego graniastosłupa jest
A) czworokąt B) pięciokąt C) sześciokąt D) dziesięciokąt
Rozwiązanie
Jeżeli w podstawie graniastosłupa jest 
–kąt to graniastosłup ma 
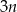krawędzi i 
ścian bocznych.
Mamy więc równanie
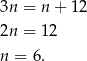
Odpowiedź: C
