Zadanie nr 4329241
Niech 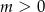 . W zależności od parametru
. W zależności od parametru 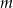 zbadaj liczbę liczb całkowitych spełniających jednocześnie nierówności
zbadaj liczbę liczb całkowitych spełniających jednocześnie nierówności 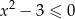 oraz
oraz 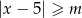 .
.
Rozwiązanie
Rozwiązaniem pierwszej nierówności jest przedział 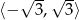 (zwykła nierówność kwadratowa). Zatem całkowite rozwiązania tej nierówności to
(zwykła nierówność kwadratowa). Zatem całkowite rozwiązania tej nierówności to 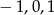 (bo
(bo 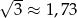 ). Mamy
). Mamy
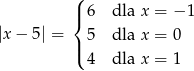
Jeżeli teraz 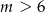 , to nierówności
, to nierówności 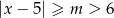 nie spełnia żadna z liczb
nie spełnia żadna z liczb 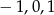 . Jeżeli
. Jeżeli 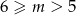 , to nierówność
, to nierówność 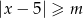 jest spełniona przez
jest spełniona przez 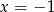 itd.
itd.
Zatem ilość całkowitych rozwiązań obu nierówności to
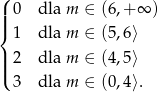
Odpowiedź: