Zadanie nr 4544920
W prostopadłościanie o objętości 3400 skrócono o 10% najkrótsze krawędzie, a następnie wydłużono najdłuższe krawędzie tak, aby otrzymany prostopadłościan miał objętość 3519. O ile procent wydłużono najdłuższe krawędzie prostopadłościanu?
A) 18% B) 12% C) 15% D) 20%
Rozwiązanie
Jeżeli oznaczymy przez 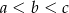 długości krawędzi prostopadłościanu to wiemy, że
długości krawędzi prostopadłościanu to wiemy, że 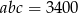 . Po pierwszej zmianie objętość prostopadłościanu jest równa
. Po pierwszej zmianie objętość prostopadłościanu jest równa
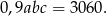
W wyniku drugiej zmiany objętość wzrasta o 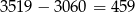 , co stanowi
, co stanowi
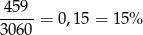
objętości przed zmianą. W takim razie najdłuższe krawędzie muszą być wydłużone o 15%.
Odpowiedź: C

