/Szkoła średnia/Zadania testowe/Geometria/Stereometria/Prostopadłościan

Zadanie nr 6921862

Dodaj do ulubionych
Dodaj do rozwiązanych

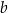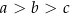Dany jest prostopadłościan o krawędziach długości a , b i c , gdzie a > b > c . Suma długości wszystkich krawędzi tego prostopadłościanu jest równa 116. Pole powierzchni całkowitej prostopadłościanu jest równe 552. Dokończ zdanie. Wybierz dwie właściwe odpowiedzi spośród podanych.
Zależności między długościami krawędzi tego prostopadłościanu zapisano w układzie równań
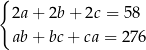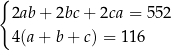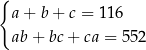
A) { 2a+ 2b+ 2c = 58 ab+ bc+ ca = 276 B) { 2ab+ 2bc+ 2ca = 552 4(a+ b+ c) = 116 C) { a+ b+ c = 116 ab+ bc+ ca = 552

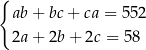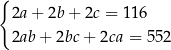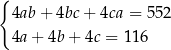
D) { ab+ bc+ ca = 552 2a+ 2b+ 2c = 58 E) { 2a+ 2b+ 2c = 116 2ab+ 2bc+ 2ca = 552 F) { 4ab + 4bc + 4ca = 552 4a + 4b + 4c = 116

Rozwiązanie

Szkicujemy prostopadłościan.

ZINFO-FIGURE

Informacja o sumie wszystkich krawędzi prostopadłościanu oznacza, że

116 = 4a+ 4b + 4c / : 2 58 = 2a+ 2b + 2c / : 2 29 = a+ b+ c.

Informacja o polu powierzchni całkowitej oznacza, że

552 = 2ab + 2bc + 2ca / : 2 276 = ab + bc + ca.

 
Odpowiedź: A, B

Wersja PDF