/Szkoła średnia/Zadania testowe/Geometria/Stereometria/Prostopadłościan

Zadanie nr 7002866

Stosunek długości trzech krawędzi prostopadłościanu o objętości 240 jest równy 2:3:5. Pole powierzchni tego prostopadłościanu jest równe:
A) 124 B) 248 C) 496 D) 62

Wersja PDF

Rozwiązanie

Powiedzmy, że krawędzie prostopadłościanu mają długości: 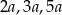2a ,3a,5a .

PIC

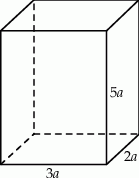
Z podanej objętości mamy

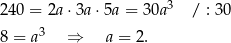
3 240 = 2a⋅3a ⋅5a = 30a / : 30 8 = a3 ⇒ a = 2.

Pole powierzchni prostopadłościanu jest więc równe

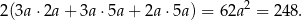
2 2(3a ⋅2a + 3a ⋅5a + 2a ⋅5a) = 62a = 248.

 
Odpowiedź: B

Wersja PDF