Zadanie nr 6597583
Wskaż 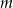 , dla którego istnieją co najmniej dwie różne liczby
, dla którego istnieją co najmniej dwie różne liczby 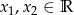 spełniające równanie
spełniające równanie 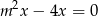 .
.
A) 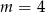 B)
B) 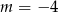 C)
C) 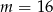 D)
D) 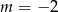
Rozwiązanie
Wykresem lewej strony równania jest prosta 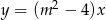 . Jeżeli prosta ta ma przecinać oś
. Jeżeli prosta ta ma przecinać oś 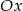 w co najmniej w dwóch punktach, to musi być pozioma, czyli
w co najmniej w dwóch punktach, to musi być pozioma, czyli
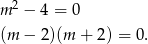
Wśród podanych liczb tylko 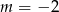 spełnia ten warunek.
spełnia ten warunek.
Odpowiedź: D

