/Szkoła średnia/Zadania testowe/Ciągi/Geometryczny

Zadanie nr 3290308

Dodaj do ulubionych
Dodaj do rozwiązanych

Dany jest ciąg geometryczny o wyrazie ogólnym 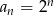n an = 2 , gdzie 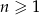n ≥ 1 . Liczba wyrazów tego ciągu mniejszych od 128 jest równa
A) 6 B) 5 C) 4 D) 7

Rozwiązanie

Sposób I

Liczymy kolejne wyrazy tego ciągu

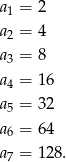
a1 = 2 a2 = 4 a3 = 8 a = 16 4 a5 = 32 a = 64 6 a7 = 128.

Widać, że wyrazów mniejszych od 128 jest 6.

Sposób II

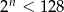Sprawdzamy jakie n spełniają nierówność 2n < 128 .

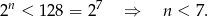
n 7 2 < 128 = 2 ⇒ n < 7 .

Liczby naturalne dodatnie spełniające powyższą nierówność, to 1,2,3,4,5,6.  
Odpowiedź: A

Wersja PDF