Zadanie nr 6542183
Dany jest ciąg geometryczny 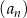 , określony dla
, określony dla 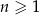 , w którym
, w którym 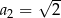 ,
, 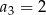 . Suma sześciu początkowych wyrazów ciągu
. Suma sześciu początkowych wyrazów ciągu 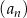 jest równa
jest równa
A) 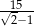 B)
B) 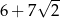 C)
C) 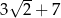 D)
D) 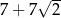
Rozwiązanie
Liczymy iloraz ciągu
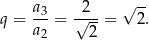
Sposób I
Obliczamy sześć pierwszych wyrazów ciągu 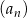 .
.
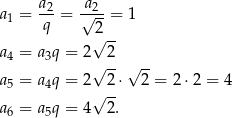
Stąd
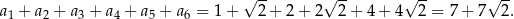
Sposób II
Korzystamy ze wzoru na sumę 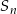 kolejnych wyrazów ciągu geometrycznego
kolejnych wyrazów ciągu geometrycznego
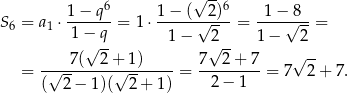
Odpowiedź: D

