Zadanie nr 8269974
Dany jest nieskończony ciąg geometryczny, w którym suma wszystkich wyrazów jest 4 razy większa od sumy wszystkich wyrazów o numerach parzystych. Iloraz tego ciągu jest równy
A) 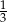 B)
B) 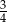 C) 1 D)
C) 1 D) 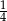
Rozwiązanie
Jeżeli oznaczymy przez 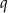 szukany iloraz ciągu
szukany iloraz ciągu 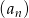 , to wyrazy tego ciągu o numerach parzystych tworzą ciąg geometryczny o pierwszym wyrazie równym
, to wyrazy tego ciągu o numerach parzystych tworzą ciąg geometryczny o pierwszym wyrazie równym 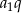 i ilorazie
i ilorazie 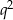 . Mamy więc równanie
. Mamy więc równanie
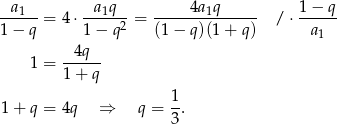
Odpowiedź: A

