Zadanie nr 8553520
Liczba 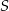 jest sumą wszystkich wyrazów nieskończonego ciągu geometrycznego o pierwszym wyrazie równym
jest sumą wszystkich wyrazów nieskończonego ciągu geometrycznego o pierwszym wyrazie równym 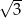 i ilorazie
i ilorazie 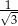 . Liczba
. Liczba 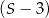 jest sumą wszystkich wyrazów nieskończonego ciągu geometrycznego o pierwszym wyrazie równym
jest sumą wszystkich wyrazów nieskończonego ciągu geometrycznego o pierwszym wyrazie równym 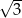 i ilorazie
i ilorazie 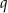 . Wynika stąd, że liczba
. Wynika stąd, że liczba 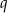 jest równa
jest równa
A) 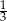 B)
B) 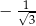 C)
C) 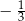 D)
D) 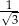
Rozwiązanie
Zauważmy najpierw, że
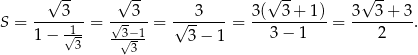
W takim razie suma drugiego z opisanych szeregów geometrycznych jest równa
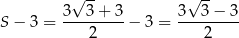
i musimy rozwiązać równanie
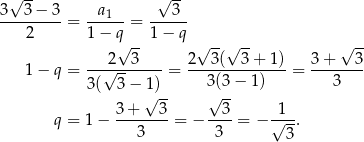
Odpowiedź: B

