/Szkoła średnia/Zadania testowe/Prawdopodobieństwo

Zadanie nr 2022611

Dodaj do ulubionych
Dodaj do rozwiązanych

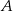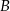Niepuste zdarzenia losowe A i B zawarte w 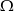Ω są takie, że 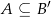′ A ⊆ B , gdzie 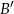B ′ oznacza zdarzenie przeciwne do zdarzenia 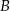B . Wynika stąd, że
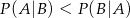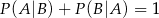
A) P (A|B ) < P(B |A ) B) P (A |B )+ P(B |A ) = 1
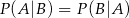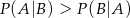
C) P(A |B) = P(B |A ) D) P(A |B) > P (B|A )

Rozwiązanie

Szkicujemy sytuację opisaną w treści zadania.

PIC

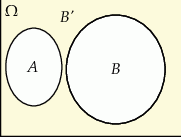
Wiemy, że

A ⊆ B′ ⇒ A ∩ B = ∅ .

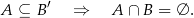
Stąd

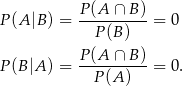
P (A |B ) = P-(A-∩-B-)= 0 P (B) P (A ∩ B ) P (B|A ) = ----------= 0. P (A )

 
Odpowiedź: C

Wersja PDF