Zadanie nr 1508396
Ze zbioru cyfr 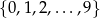 losujemy dwa razy po jednej cyfrze bez zwracania. Prawdopodobieństwo, że wylosowane cyfry (w kolejności losowania) utworzą liczbę podzielną przez 5 jest równe
losujemy dwa razy po jednej cyfrze bez zwracania. Prawdopodobieństwo, że wylosowane cyfry (w kolejności losowania) utworzą liczbę podzielną przez 5 jest równe
A) 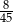 B)
B) 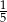 C)
C)  D)
D) 
Rozwiązanie
Obliczamy liczbę wszystkich zdarzeń
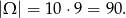
Oznaczmy przez 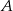 zbiór zdarzeń sprzyjających. Pamiętamy, że liczba jest podzielna przez 5 jeżeli cyfra jedności tej liczby to 0 lub 5. Wszystkie zdarzenia sprzyjające podzielimy na dwa zbiory
zbiór zdarzeń sprzyjających. Pamiętamy, że liczba jest podzielna przez 5 jeżeli cyfra jedności tej liczby to 0 lub 5. Wszystkie zdarzenia sprzyjające podzielimy na dwa zbiory 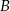 i
i 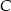 . Pierwszy będzie składać się z tych zdarzeń sprzyjających, w których w pierwszym losowaniu wylosowaliśmy cyfrę różną od 0 i 5 – w takiej sytuacji w drugim musieliśmy wylosować jedną z liczb 0 lub 5. Zatem
. Pierwszy będzie składać się z tych zdarzeń sprzyjających, w których w pierwszym losowaniu wylosowaliśmy cyfrę różną od 0 i 5 – w takiej sytuacji w drugim musieliśmy wylosować jedną z liczb 0 lub 5. Zatem
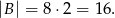
Drugi składa się z tych zdarzeń sprzyjających, w których w pierwszym losowaniu wylosowaliśmy 0 lub 5 – wówczas w drugim musieliśmy wylosować jedną z liczb 0 lub 5, której nie wylosowaliśmy w pierwszym losowaniu. Zatem
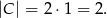
Stąd
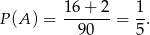
Odpowiedź: B

