Zadanie nr 3915374
Ze zbioru liczb naturalnych zawartych w przedziale 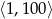 wybieramy losowo jedną. Niech
wybieramy losowo jedną. Niech 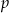 oznacza prawdopodobieństwo wylosowania liczby będącej wielokrotnością liczby 7. Wówczas
oznacza prawdopodobieństwo wylosowania liczby będącej wielokrotnością liczby 7. Wówczas
A) 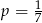 B)
B) 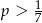 C)
C) 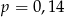 D)
D) 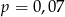
Rozwiązanie
Sposób I
Policzmy ile jest liczb podzielnych przez 7 w przedziale 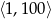 . Są to liczby
. Są to liczby
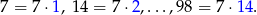
Jest więc 14 takich liczb i prawdopodobieństwo wynosi
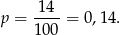
Sposób II
Możemy wpisać wszystkie liczby podzielne przez 7 i zawarte w przedziale 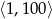 .
.
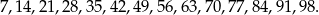
Widać, że jest ich 14. Zatem
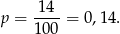
Odpowiedź: C

