Zadanie nr 4120108
Ze zbioru trzycyfrowych liczb naturalnych wybieramy losowo jedną liczbę. Prawdopodobieństwo otrzymania liczby podzielnej przez 30 jest równe
A) 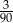 B)
B) 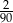 C)
C) 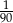 D)
D) 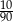
Rozwiązanie
Liczb trzycyfrowych jest
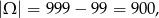
(od liczby liczb mniejszych od 1000 odejmujemy liczbę tych, które są mniejsze od 100). Najmniejszą liczbą trzycyfrową podzielną przez 3 jest
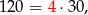
a największą
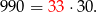
Zatem liczb trzycyfrowych podzielnych przez 30 jest tyle, ile liczb od 4 do 33, czyli 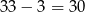 .
.
Prawdopodobieństwo jest więc równe
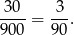
Odpowiedź: A

