Zadanie nr 5985510
Ze zbioru liczb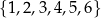 
losujemy dwa razy po jednej liczbie ze zwracaniem. Wybierz P, jeśli zdanie jest prawdziwe, lub F – jeśli jest fałszywe.
| Prawdopodobieństwo wylosowania dwóch liczb, których suma dzieli się przez 9 jest większe od 0,1. | P | F |
| Prawdopodobieństwo tego, że pierwsza liczba dzieli drugą jest mniejsze niż 0,38. | P | F |
Rozwiązanie
Rozwiązanie tego zadania jest dostępne tylko dla użytkowników z wykupionym abonamentem.
Nie chcesz się rejestrować ani opłacać abonamentu? Zapłać przelewem 7,90 zł lub telefonicznie 9,90 zł, a otrzymasz dwudziestominutowy dostęp do wszystkich materiałów dostępnych w portalu.
