Zadanie nr 8330241
Ze zbioru cyfr 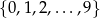 losujemy dwa razy po jednej cyfrze bez zwracania. Prawdopodobieństwo, że wybrane w kolejności losowania cyfry utworzą dwucyfrową liczbę parzystą, jest równe
losujemy dwa razy po jednej cyfrze bez zwracania. Prawdopodobieństwo, że wybrane w kolejności losowania cyfry utworzą dwucyfrową liczbę parzystą, jest równe
A) 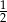 B)
B) 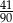 C)
C)  D)
D) 
Rozwiązanie
Obliczamy liczbę wszystkich zdarzeń
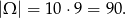
Oznaczmy przez 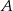 zbiór zdarzeń sprzyjających. Pamiętamy, że liczba jest podzielna przez 2 jeżeli cyfra jedności tej liczby jest parzysta. W zbiorze
zbiór zdarzeń sprzyjających. Pamiętamy, że liczba jest podzielna przez 2 jeżeli cyfra jedności tej liczby jest parzysta. W zbiorze 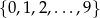 liczbami parzystymi są 0,2,4,6,8. Wszystkie zdarzenia sprzyjające podzielimy na dwa zbiory
liczbami parzystymi są 0,2,4,6,8. Wszystkie zdarzenia sprzyjające podzielimy na dwa zbiory 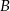 i
i 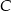 . Pierwszy będzie składać się z tych zdarzeń sprzyjających, w których w pierwszym losowaniu wylosowaliśmy liczbę nieparzystą – w takiej sytuacji w drugim musieliśmy wylosować jedną z liczb 0,2,4,6,8. Zatem
. Pierwszy będzie składać się z tych zdarzeń sprzyjających, w których w pierwszym losowaniu wylosowaliśmy liczbę nieparzystą – w takiej sytuacji w drugim musieliśmy wylosować jedną z liczb 0,2,4,6,8. Zatem
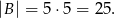
Drugi składa się z tych zdarzeń sprzyjających, w których w pierwszym losowaniu wylosowaliśmy liczbę parzystą (nie może być 0!) – wówczas w drugim musieliśmy wylosować jedną z liczb parzystych, której nie wylosowaliśmy w pierwszym losowaniu. Zatem
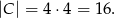
Stąd
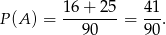
Odpowiedź: B

