Zadanie nr 6851226
Zdarzenia 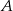 i
i 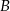 zawarte w zbiorze zdarzeń elementarnych
zawarte w zbiorze zdarzeń elementarnych 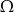 spełniają warunek
spełniają warunek 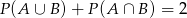 . Zatem
. Zatem
A) 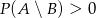 B)
B) 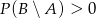 C)
C) 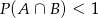 D)
D) 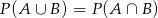
Rozwiązanie
Sposób I
Ponieważ prawdopodobieństwo zawsze jest nie większe niż 1, podany warunek oznacza, że oba prawdopodobieństwa z lewej strony równości muszą być równe 1, czyli
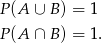
Sposób II
Korzystając ze wzoru
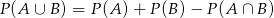
mamy
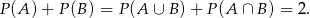
Tak jak w poprzednim sposobie zauważamy, że powyższy warunek oznacza, że
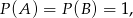
czyli 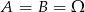 .
.
Odpowiedź: D

