Zadanie nr 5973493
Przekątne dzielą równoległobok na cztery trójkąty
A) przystające B) podobne C) o równych polach D) o równych obwodach
Rozwiązanie
Szkicujemy równoległobok.
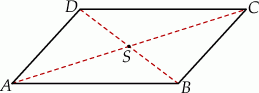
Ponieważ przekątne równoległoboku dzielą się na połowy, trójkąty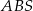 
i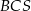 
mają równe podstawy 
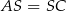oraz wspólną wysokość opuszczoną z wierzchołka 
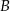na przekątną 
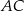. W takim razie mają równe pola. Ponadto trójkąt 
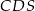jest przystający do trójkąta 
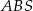, a trójkąt 
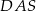jest przystający do trójkąta 
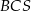. To oznacza, że te wszystkie cztery trójkąty mają równe pola.
Z drugiej strony, trójkąty te nie muszą być podobne, ani nie muszą mieć równych obwodów. Tym bardziej nie muszą być przystające.
Odpowiedź: C
