Zadanie nr 9722447
Z przeciwległych wierzchołków kwadratu o boku 2 zatoczono koła o promieniu 2. Pole części wspólnej tych kół jest równe
A) 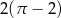 B)
B) 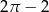 C)
C) 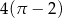 D)
D) 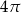
Rozwiązanie
Zaczynamy od rysunku
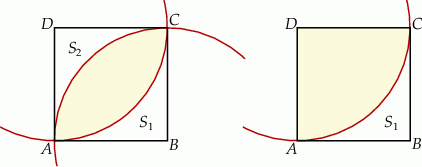
Zauważmy, że pole powierzchni części wspólnej koła i kwadratu jest równa 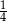 pola powierzchni koła. Obliczymy teraz pole powierzchni
pola powierzchni koła. Obliczymy teraz pole powierzchni 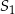
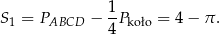
Figura 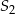 jest symetrycznym odbiciem figury
jest symetrycznym odbiciem figury 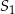 , więc ma takie same pole
, więc ma takie same pole
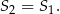
Teraz już łatwo obliczyć poszukiwane pole powierzchni
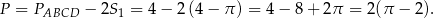
Odpowiedź: A

