Zadanie nr 5714689
Pole równoległoboku 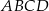 jest równe 120. Na bokach
jest równe 120. Na bokach 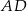 i
i 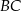 wybrano – odpowiednio – punkty
wybrano – odpowiednio – punkty 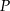 i
i 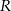 , takie, że
, takie, że 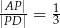 i
i 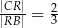 (zobacz rysunek)
(zobacz rysunek)
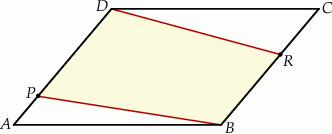
Pole czworokąta 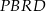 jest równe
jest równe
A) 81 B) 96 C) 102 D) 118
Rozwiązanie
Czworokąt 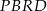 jest trapezem o podstawach
jest trapezem o podstawach
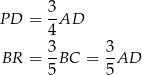
oraz wysokości 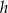 takiej samej jak wysokość równoległoboku opuszczona na podstawę
takiej samej jak wysokość równoległoboku opuszczona na podstawę 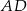 . Jego pole jest więc równe
. Jego pole jest więc równe
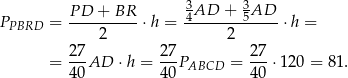
Odpowiedź: A

