Zadanie nr 8850899
Boki równoległoboku  mają długości 2 i 5, a jego dłuższa przekątna ma długość 6.
mają długości 2 i 5, a jego dłuższa przekątna ma długość 6.
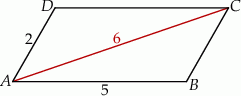
Pole tego równoległoboku jest równe
A) 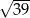 B) 48 C)
B) 48 C) 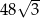 D)
D) 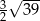
Rozwiązanie
Sposób I
Korzystamy ze wzoru Herona
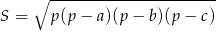
na pole trójkąta o bokach 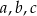 i połowie obwodu
i połowie obwodu 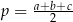 . W trójkącie
. W trójkącie 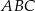 mamy
mamy
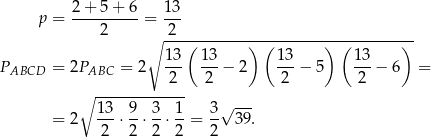
Sposób II
Oznaczmy przez  kąt rozwarty równoległoboku. Na mocy twierdzenia cosinusów w trójkącie
kąt rozwarty równoległoboku. Na mocy twierdzenia cosinusów w trójkącie 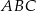 mamy
mamy
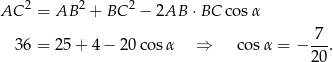
Stąd
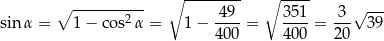
i pole równoległoboku jest równe
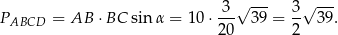
Odpowiedź: D

