/Szkoła średnia/Zadania testowe/Geometria/Planimetria/Czworokąt/Równoległobok

Zadanie nr 9690600

Dodaj do ulubionych
Dodaj do rozwiązanych

Przekątne podzieliły równoległobok na cztery trójkąty o polach 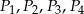P1,P2,P3,P 4 .

PIC

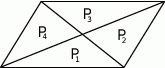
Który z podanych warunków może nie być spełniony?
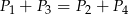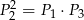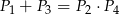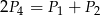
A) P1 + P3 = P2 + P4 B) P22= P1 ⋅ P3 C) P + P = P ⋅P 1 3 2 4 D) 2P 4 = P1 + P2

Rozwiązanie

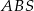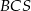Ponieważ przekątne równoległoboku dzielą się na połowy, trójkąty ABS i BCS mają równe podstawy 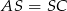AS = SC oraz wspólną wysokość opuszczoną z wierzchołka 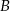B na przekątną AC .

PIC

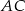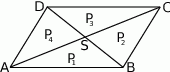
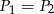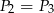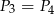Zatem P1 = P2 . Podobnie uzasadniamy, że P2 = P3 i P3 = P4 , czyli wszystkie cztery liczby 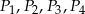P 1,P 2,P3,P4 są równe. W takim razie na pewno spełnione są warunki.

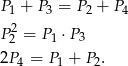
P1 + P3 = P2 + P4 2 P2 = P1 ⋅ P3 2P 4 = P1 + P2.

Natomiast warunek 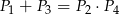P + P = P ⋅P 1 3 2 4 nie musi być spełniony.  
Odpowiedź: C

Wersja PDF