Zadanie nr 2912310
- Narysuj wykresy funkcji
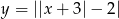 oraz
oraz 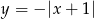 , gdzie
, gdzie 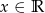 .
. - Wyznacz te wartości parametru
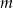 , dla których równanie
, dla których równanie 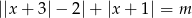 ma dokładnie dwa rozwiązania.
ma dokładnie dwa rozwiązania.
Rozwiązanie
- Aby narysować wykres pierwszej funkcji startujemy od prostej
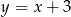 i odbijamy część pod osią
i odbijamy część pod osią 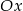 do góry, otrzymujemy w ten sposób
do góry, otrzymujemy w ten sposób 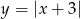 . Teraz przesuwamy ten wykres o 2 jednostki w dół (mamy
. Teraz przesuwamy ten wykres o 2 jednostki w dół (mamy 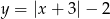 ) i ponownie odbijamy część poniżej osi
) i ponownie odbijamy część poniżej osi 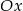 do góry.
do góry. Aby naszkicować drugi wykres, rozpoczynamy od prostej
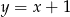 i odbijamy część poniżej osi
i odbijamy część poniżej osi 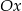 do góry, otrzymujemy w ten sposób wykres funkcji
do góry, otrzymujemy w ten sposób wykres funkcji 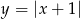 . Na koniec odbijamy cały wykres względem osi
. Na koniec odbijamy cały wykres względem osi 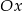 .
. 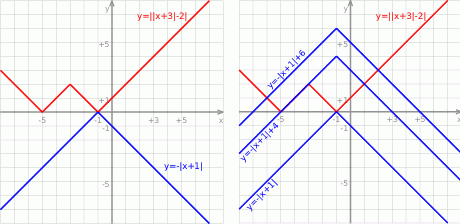
Odpowiedź: Wykresy - O danym równaniu myślimy w postaci
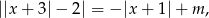
czyli pierwszy wykres stoi w miejscu, a drugi przesuwamy wzdłuż osi
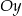 . Jeżeli
. Jeżeli 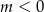 to oba wykresy są rozłączne, a jeżeli
to oba wykresy są rozłączne, a jeżeli 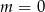 to mają dokładnie jeden punkt wspólny. Jeżeli
to mają dokładnie jeden punkt wspólny. Jeżeli 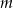 zaczyna być dodatnie, to wykresy mają dwa punkty wspólne, z wyjątkiem wartości
zaczyna być dodatnie, to wykresy mają dwa punkty wspólne, z wyjątkiem wartości 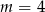 , kiedy to kawałki wykresów się pokrywają i dane równanie ma nieskończenie wiele rozwiązań. Zatem
, kiedy to kawałki wykresów się pokrywają i dane równanie ma nieskończenie wiele rozwiązań. Zatem 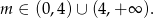
Odpowiedź: