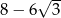Zadanie nr 6309837
Dana jest funkcja 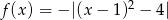 dla
dla 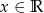 . Oblicz
. Oblicz 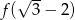 .
.
Rozwiązanie
Liczymy
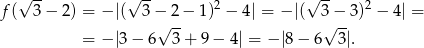
Ponieważ 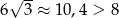 powyższe wyrażenie jest równe
powyższe wyrażenie jest równe
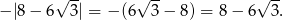
Odpowiedź: 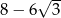
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Dana jest funkcja 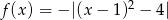 dla
dla 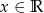 . Oblicz
. Oblicz 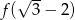 .
.
Liczymy
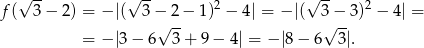
Ponieważ 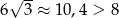 powyższe wyrażenie jest równe
powyższe wyrażenie jest równe
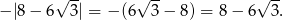
Odpowiedź: