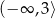/Szkoła średnia/Funkcje/Wartość bezwględna

Zadanie nr 6863997

Funkcja 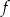f jest określona wzorem 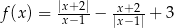|x+2| x+2-- f(x ) = x−1 − |x−1| + 3 dla każdej liczby rzeczywistej 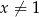x ⁄= 1 . Wyznacz zbiór jej wartości.

Wersja PDF

Rozwiązanie

Zapiszmy wzór funkcji 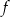f tak, aby nie było w nim wartości bezwzględnej.

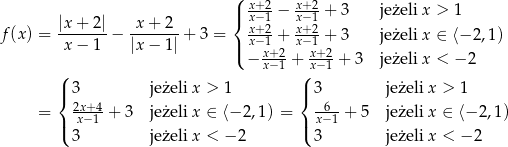
( x+2- x+-2 |x + 2| x + 2 |{ x−1 − x− 1 + 3 jeżeli x > 1 f(x) = -------− -------+ 3 = xx+−21-+ xx+−-21 + 3 jeżeli x ∈ ⟨− 2,1) x − 1 |x − 1 | |( x+2- x+-2 ( − x−1 +(x− 1 + 3 jeżeli x < − 2 | 3 jeżeli x > 1 | 3 jeżeli x > 1 { 2x+4 { 6 = | x−-1-+ 3 jeżeli x ∈ ⟨− 2,1) = | x−-1 + 5 jeżeli x ∈ ⟨− 2,1) ( 3 jeżeli x < −2 ( 3 jeżeli x < − 2

Szkicujemy teraz wykres funkcji 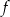f .

PIC

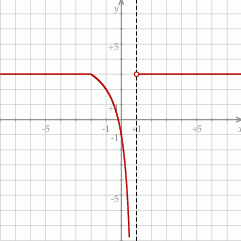
Z wykresu widać, że zbiorem wartości funkcji 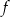f jest przedział:

(− ∞ ,3⟩.

 
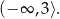
Odpowiedź: (− ∞ ,3⟩

Wersja PDF