Zadanie nr 9685193
Oblicz 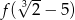 jeżeli
jeżeli 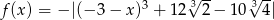 .
.
Rozwiązanie
Liczymy
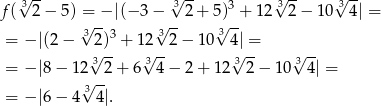
Pozostało ustalić jaki jest znak wyrażenia pod wartością bezwzględną. Zauważmy, że 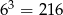 oraz
oraz 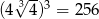 . Zatem druga liczba jest większa i mamy
. Zatem druga liczba jest większa i mamy
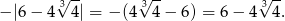
Odpowiedź: 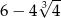
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Oblicz 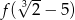 jeżeli
jeżeli 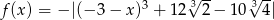 .
.
Liczymy
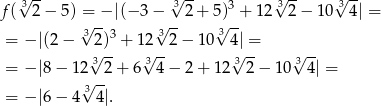
Pozostało ustalić jaki jest znak wyrażenia pod wartością bezwzględną. Zauważmy, że 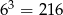 oraz
oraz 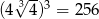 . Zatem druga liczba jest większa i mamy
. Zatem druga liczba jest większa i mamy
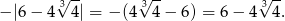
Odpowiedź: