/Szkoła średnia/Zadania testowe/Ciągi/Dowolny

Zadanie nr 4521549

Dodaj do ulubionych
Dodaj do rozwiązanych

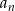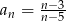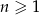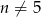Ciąg an dany jest wzorem n−3- an = n−5 , gdzie n ≥ 1 oraz n ⁄= 5 . Liczba wyrazów całkowitych tego ciągu to
A) 1 B) 2 C) 3 D) 4

Rozwiązanie

Sposób I

Jeżeli zapiszemy wyraz ciągu w postaci

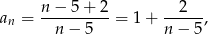
an = n-−-5-+-2-= 1 + --2---, n − 5 n − 5

to widać, że 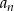an będzie liczbą całkowitą tylko wtedy, gdy 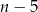n − 5 dzieli 2, czyli 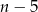n − 5 musi być jedną z liczb 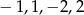− 1,1,− 2,2 . Tak będzie gdy

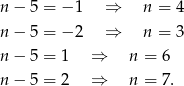
n − 5 = − 1 ⇒ n = 4 n − 5 = − 2 ⇒ n = 3 n − 5 = 1 ⇒ n = 6 n − 5 = 2 ⇒ n = 7.

Zatem cztery wyrazy ciągu są liczbami całkowitymi.

Sposób II

Liczymy kolejne wyrazy ciągu

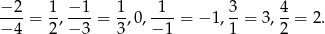
− 2 1 − 1 1 1 3 4 −-4-= 2,−-3-= 3,0,−-1-= − 1,1-= 3,2-= 2.

Dalej nie mamy po co liczyć, bo widać, że są co najmniej cztery wyrazy całkowite.  
Odpowiedź: D

Wersja PDF