Zadanie nr 8083518
Wyraz ogólny ciągu 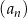 ma postać
ma postać 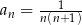 , gdzie
, gdzie 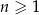 . Wobec tego
. Wobec tego
A) 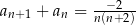 B)
B) 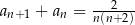
C) 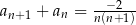 D)
D) 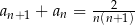
Rozwiązanie
Liczymy
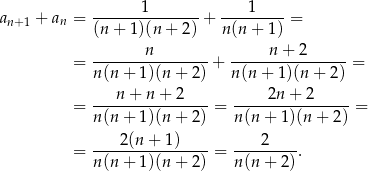
Odpowiedź: B
 Największy internetowy zbiór zadań z matematyki
Największy internetowy zbiór zadań z matematyki
Wyraz ogólny ciągu 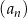 ma postać
ma postać 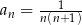 , gdzie
, gdzie 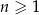 . Wobec tego
. Wobec tego
A) 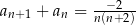 B)
B) 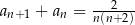
C) 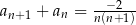 D)
D) 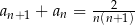
Liczymy
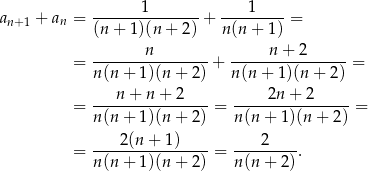
Odpowiedź: B
