/Szkoła średnia/Zadania testowe/Funkcje/Kwadratowa

Zadanie nr 5040573

Dodaj do ulubionych
Dodaj do rozwiązanych

Największa wartość funkcji kwadratowej 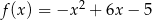2 f(x) = −x + 6x − 5 w przedziale 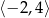⟨− 2,4⟩ jest równa
A) 35 B) 22 C) 4 D) 3

Rozwiązanie

Sposób I

Obliczmy pierwszą współrzędną wierzchołka paraboli będącej wykresem funkcji 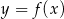y = f(x) .

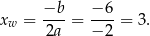
−b-- −-6- xw = 2a = − 2 = 3.

Wierzchołek znajduje się w podanym przedziale, więc to w nim funkcja przyjmuje wartość największą i jest ona równa

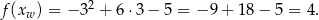
f(x ) = − 32 + 6⋅ 3− 5 = − 9+ 18− 5 = 4. w

Sposób II

Zapiszmy podaną funkcję w postaci kanonicznej

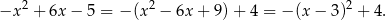
2 2 2 −x + 6x − 5 = − (x − 6x+ 9)+ 4 = − (x − 3) + 4.

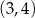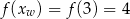Widać stąd, że wierzchołek paraboli będącej wykresem tej funkcji ma współrzędne (3,4) , czyli największa wartość funkcji to f (xw) = f (3) = 4 .

Na koniec wykres funkcji y = f (x) .

PIC

 
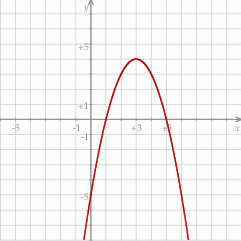
Odpowiedź: C

Wersja PDF