/Szkoła średnia/Zadania testowe/Funkcje/Kwadratowa

Zadanie nr 6045405

Dodaj do ulubionych
Dodaj do rozwiązanych

Zbiorem wartości funkcji kwadratowej 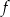f określonej wzorem 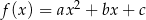2 f(x ) = ax + bx + c jest przedział 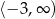⟨− 3,∞ ) , a rozwiązaniem nierówności 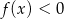f(x ) < 0 jest przedział 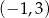(− 1,3) . Wskaż wzór funkcji f .
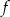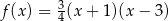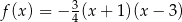
A) f (x) = 3(x + 1 )(x − 3) 4 B) 3 f (x) = − 4(x + 1)(x − 3 )
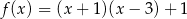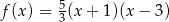
C) f(x ) = (x+ 1)(x − 3) + 1 D) f (x) = 53(x + 1)(x − 3 )

Rozwiązanie

Ponieważ funkcja 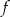f przyjmuje wartość najmniejszą -3, więc ramiona jej wykresu muszą być skierowane ku górze. To eliminuje odpowiedź z ujemnym współczynnikiem przy x2 .

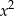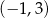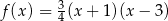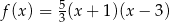Wiemy ponadto, że funkcja przyjmuje wartości ujemne dokładnie na przedziale (− 1,3) , więc liczby -1 i 3 muszą być jej miejscami zerowymi. To ogranicza możliwe odpowiedzi do 3 f (x) = 4(x + 1)(x − 3) i f (x) = 53(x + 1)(x − 3 ) . W obu przypadkach wierzchołek paraboli znajduje się dokładnie w środku pomiędzy pierwiastkami, czyli jego pierwsza współrzędna jest równa

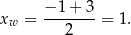
− 1+ 3 xw = ---2--- = 1.

Aby rozpoznać poprawną odpowiedź wystarczy teraz sprawdzić, dla której funkcji zachodzi równość

f(xw ) = − 3.

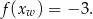
Gdy to zrobimy okaże się, że tak jest dla funkcji 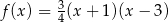3 f(x) = 4(x+ 1)(x− 3) .

Na koniec obrazek.

PIC

 
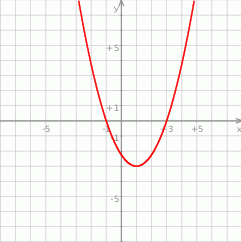
Odpowiedź: A

Wersja PDF