Zadanie nr 6277370
Jeśli funkcja kwadratowa 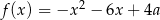 ma dwa miejsca zerowe, to liczba
ma dwa miejsca zerowe, to liczba  spełnia warunek
spełnia warunek
A) 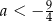 B)
B) 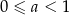 C)
C) 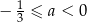 D)
D) 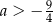
Rozwiązanie
Sposób I
Zapiszmy wzór funkcji 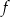 w postaci kanonicznej
w postaci kanonicznej
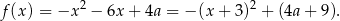
Wykresem tej funkcji jest więc parabola o ramionach skierowanych w dół i wierzchołku w punkcie 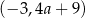 . Jeżeli funkcja ma dwa miejsca zerowe, to jej wykres musi przecinać oś
. Jeżeli funkcja ma dwa miejsca zerowe, to jej wykres musi przecinać oś 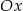 , tzn.
, tzn.

Sposób II
Wiemy, że równanie
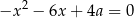
ma dwa rozwiązania, więc musi być
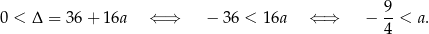
Sposób III
Wykresem funkcji 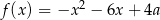 jest parabola o ramionach skierowanych w dół i pierwszej współrzędnej wierzchołka równej
jest parabola o ramionach skierowanych w dół i pierwszej współrzędnej wierzchołka równej
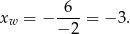
Jeżeli funkcja ma mieć dwa miejsca zerowe, to jej wykres musi przecinać oś 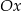 , tzn.
, tzn.
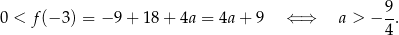
Odpowiedź: D

