/Szkoła średnia/Zadania testowe/Funkcje/Kwadratowa

Zadanie nr 6364338

Dodaj do ulubionych
Dodaj do rozwiązanych

Najmniejszą wartością funkcji 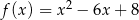2 f (x) = x − 6x + 8 w przedziale 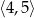⟨4,5⟩ jest
A) 0 B) 3 C) 9 D) -16

Rozwiązanie

Wykres podanej funkcji kwadratowej jest parabolą o ramionach skierowanych w górę, zatem wartość najmniejszą przyjmuje albo w wierzchołku (jeżeli należy on do podanego zbioru), albo w jednym z końców przedziału. Przypomnijmy, że współrzędne wierzchołka paraboli są dana wzorem

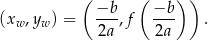
( ( ) ) −b-- −b-- (xw,yw ) = 2a ,f 2a .

W naszej sytuacji

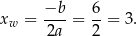
−b 6 xw = 2a-= 2-= 3.

i wierzchołek nie należy do zbioru 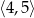⟨4,5 ⟩ . Liczymy wartości w końcach przedziału

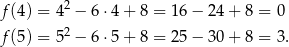
f(4 ) = 42 − 6⋅4 + 8 = 16− 24+ 8 = 0 f(5 ) = 52 − 6⋅5 + 8 = 25− 30+ 8 = 3.

Zatem najmniejsza wartość to 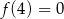f(4) = 0 .

Na koniec obrazek

PIC

 
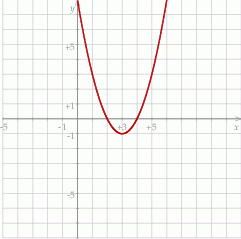
Odpowiedź: A

Wersja PDF