/Szkoła średnia/Zadania testowe/Funkcje/Kwadratowa

Zadanie nr 6735922

Dodaj do ulubionych
Dodaj do rozwiązanych

Zbiorem wartości funkcji 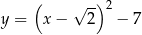( √ --)2 y = x − 2 − 7 określonej w przedziale 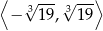⟨ √3---√3---⟩ − 19, 1 9 jest
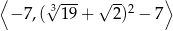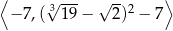
A) ⟨ √3--- √ --2 ⟩ − 7,( 19 + 2) − 7 B) ⟨ ⟩ √3--- √ --2 − 7,( 19 − 2) − 7
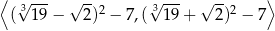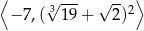
C) ⟨ ⟩ ( 3√ 19-− √ 2)2 − 7,(√319-+ √ 2)2 − 7 D) ⟨ --- -- ⟩ − 7,(√319 + √ 2)2

Rozwiązanie

Sposób I

Zauważmy, że pierwsza współrzędna wierzchołka danej paraboli

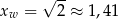
√ -- xw = 2 ≈ 1,41

znajduje się w podanym przedziale, więc na pewno najmniejszą wartością jest 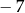− 7 .

PIC

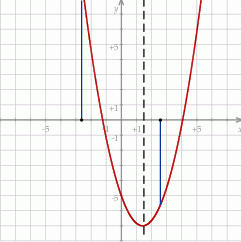
Ponadto, oś symetrii paraboli znajduje się po prawej stronie środka danego przedziału, więc większą wartość przyjmuje ta parabola w lewym końcu przedziału, niż w prawym. Zatem największa wartość to

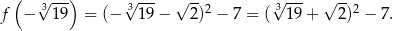
( √3--) 3√ --- √ --2 √3--- √ -- 2 f − 19 = (− 19 − 2) − 7 = ( 19 + 2 ) − 7.

Sposób II

Sprawdzamy podane odpowiedzi. Jak w poprzednim sposobie zauważamy, że najmniejsza wartość to 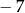− 7 . Ponadto

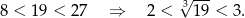
--- 8 < 1 9 < 27 ⇒ 2 < 3√ 19 < 3.

Stąd

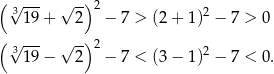
( 3√ --- √ -)2 2 19+ 2 − 7 > (2 + 1) − 7 > 0 ( 3√ --- √ -)2 19− 2 − 7 < (3 − 1)2 − 7 < 0 .

Zatem największą wartością musi być pierwsza z tych liczb.  
Odpowiedź: A

Wersja PDF