/Szkoła średnia/Zadania testowe/Funkcje/Kwadratowa

Zadanie nr 7233476

Jeżeli miejscami zerowymi funkcji kwadratowej są liczby 6 oraz -2, a wierzchołek paraboli będącej jej wykresem ma współrzędne 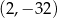(2,− 32 ) , to wzór tej funkcji można zapisać w postaci
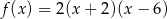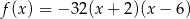
A) f (x) = 2(x + 2)(x − 6) B) f (x) = − 32(x + 2)(x − 6)
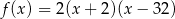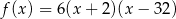
C) f(x ) = 2(x + 2)(x − 32) D) f (x) = 6(x + 2)(x − 32 )

Wersja PDF

Rozwiązanie

Sposób I

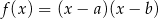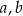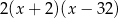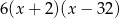Pierwiastkami funkcji kwadratowej f (x) = (x − a)(x − b) są liczby a,b . Zatem od razu odpadają funkcje 2(x+ 2)(x − 32) i 6(x + 2)(x − 3 2) .

Żeby sprawdzić, która z pozostałych dwóch odpowiedzi jest poprawna liczymy wartości funkcji w punkcie 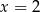x = 2 .

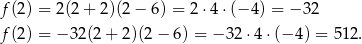
f(2) = 2(2+ 2)(2− 6) = 2 ⋅4⋅ (−4 ) = − 32 f(2) = − 32(2+ 2)(2− 6) = − 32 ⋅4 ⋅(− 4) = 512.

Widzimy zatem, że tylko funkcja 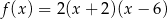f(x) = 2(x + 2 )(x− 6) spełnia założenia zadania.

Sposób II

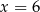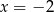Jeżeli liczby x = 6 i x = − 2 są miejscami zerowymi funkcji to jej wzór musi mieć postać

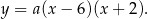
y = a(x − 6)(x + 2 ).

Współczynnik a wyznaczamy podstawiając współrzędne wierzchołka

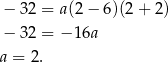
− 32 = a (2− 6)(2+ 2) − 32 = − 1 6a a = 2.

Zatem szukana funkcja to 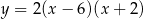y = 2(x − 6)(x + 2) .  
Odpowiedź: A

Wersja PDF