Zadanie nr 2774746
Liczba -1 jest miejscem zerowym wielomianu 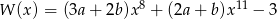 i
i 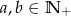 . Wynika stąd, że
. Wynika stąd, że
A)  i
i 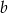 to liczby parzyste
to liczby parzyste
B) jedna z liczb 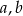 jest parzysta, a druga nieparzysta
jest parzysta, a druga nieparzysta
C)  i
i 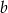 to liczby nieparzyste
to liczby nieparzyste
D) 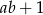 jest liczbą parzystą
jest liczbą parzystą
Rozwiązanie
Liczymy
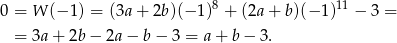
Zatem 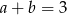 .
.
Sposób I
Jeżeli suma dwóch liczb całkowitych jest liczbą nieparzystą, to jedna z nich musi być parzysta, a druga musi być nieparzysta.
Sposób II
Liczby naturalne spełniające równanie 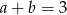 to
to
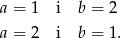
Widać, że gdy jedna z liczb jest parzysta to druga jest nieparzysta.
Odpowiedź: B

